5月18日下午，我校数学组有幸邀请到海淀区数学教研员张鹤老师，利用线上方式为我校数学教研组进行讲座。张鹤老师首先对如何进行更高效的线上教学进行了指导，并针对如何通过线上教学进一步的提升学生的思维、不让教学质量受线上形式的局限提出了四点具体的建议。

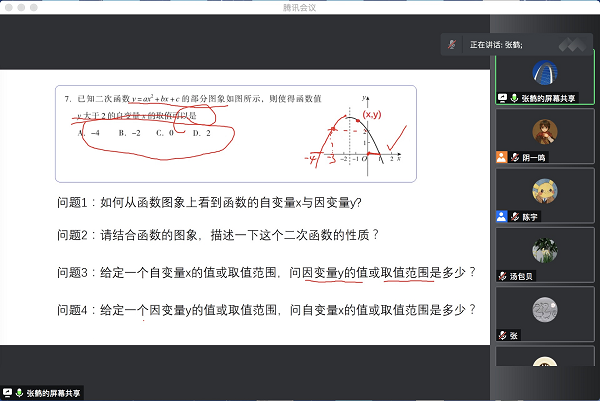
张鹤老师首先提出，在教学活动的设计中，要变“解题”为研究问题，将老师所选取的成题以问题链的形式呈现。具体操作上，可以只给出原题目的题干部分，也可以把题干中的条件拆分并按照原题干的逻辑顺序给出，在此基础上提出要解决的具体问题。在改编过程中要遵循着解决问题的逻辑，即：先理解问题、对数学问题中的具体研究对象的性质或关系进行分析，再寻找解决具体问题的方法。通过题目改编，引导学生研究问题、思考问题、解决问题。

张鹤老师给出的第二点建议是教学活动要指向学生的思维活动。张老师指出，培养学生数学思维能力的途径是理解数学能力和解决数学问题。学生需要读懂用数学语言表达的数学知识或数学问题，要能够从抽象的数学符号语言中体会到其所蕴含的丰富内涵、要能够从直观的图形语言中抽象出代数关系、要能将用文字语言表达的数学概念转化为自己的思维方式，并能用符号语言或图形语言来表达。不同的数学知识呈现出不同的思维特征，所以教师需首先理解几何思维与代数思维的特征与规律，提出聚焦思维特征的问题。解决数学问题的思维活动分为两步，第一步是对数学问题的研究对象进行研究，寻找研究对象的性质和关系的一般方法；第二步是解决数学问题中的具体问题，运用一般方法所研究出来的性质或关系探索具体解决问题的方法。

而后张鹤老师提出，教学要解释结论背后的思维。以一元二次方程是是否有实数根为例，学生对于这个问题的理解不能仅仅停留在判别式是否大于0，需要认识到我们可以将一元二次方程转化为的形式，因此当判别式小于0时方程不成立，此时无解。

张鹤老师给出的第四点建议是,希望数学一线教师以研究的状态展开自己的工作。研究知识、研究逻辑关系，化题目为问题，形成以提升学生数学思维水平为目标的数学研究课堂。同时张鹤老师对初三最后阶段的复习进行指导，他指出当前阶段复习最重要的不是知识的再确认，而是学生理解数学问题的思维水平的进一步提高、是解决数学问题思维能力的落实。

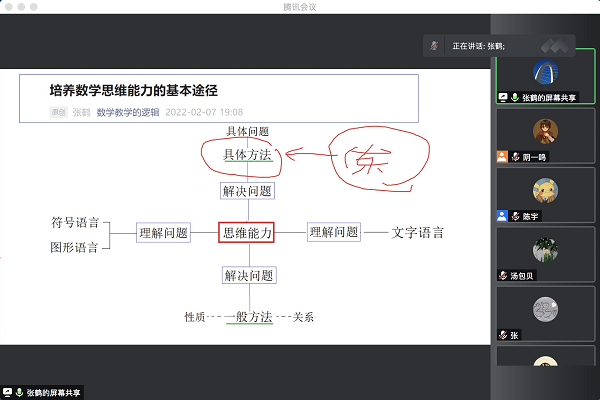
理解问题与解决问题是提升学生思维能力的关键，深刻理解数学的三种语言并把握三种语言的互相转化是理解问题的钥匙，能够在此基础之上结合条件运用一般方法与具体方法则是打开解决问题的大门。在中学阶段，学生所要学习的数学知识大致可以分为几何、代数和概率统计三个领域，在每一个领域中学生思考数学问题的思维方法是独特的，解决数学问题所运用的以数学语言为形式的数学工具也是各不相同的。如几何领域是以图形语言为主要的数学工具，所承载的是以直观为特征的几何思维；在代数领域是以数学符号语言为主要的数学工具，所承载的是以抽象为特征的代数思维；而在概率统计领域就是以数据为主的主要数学工具，所承载的是从随机性中寻找规律性为特征的不确定思维。

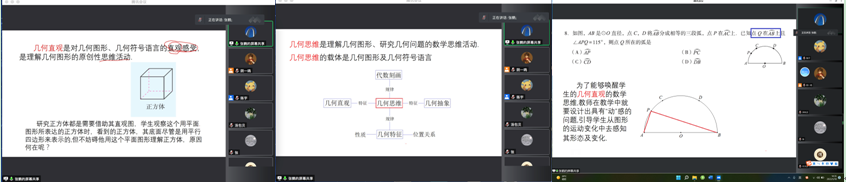
本次讲座张鹤老师对几何思维进行了详细的讲解。张老师指出，几何思维是理解几何图形、研究几何问题的数学思维活动。几何思维的载体是几何图形与几何符号语言。在几何教学中要注重对学生几何直观的培养，几何抽象能力建立在几何直观中。几何直观是对几何图形、几何符号语言的直观感受，是理解几何图形的原创性思维活动；在此基础上进行的几何抽象就是用元素间的数量关系和位置关系来刻画的图形性质。为了能够唤醒学生的几何直观的数学思维，教师在教学中要设计出具有“动”感的问题，引导学生从图形的运动变化中去感知其形态及变化。而后张老师通过具体实例讲解了如何将几何直观落实在我们的日常教学中，通过三节课堂实录说明尽管几何思维能力的培养在不同学段教学的侧重点是不同的，但几何直观是每一阶段几何能力培养的基础。

在近两个小时的讲座中，所有老师听得聚精会神，收获与感悟甚多，以下是两位老师的学习心得：

付天杰老师：张鹤老师在讲座中指出了教学中如何“教”学生学会几何思维,诠释了几何思维在几何知识教学中的价值.这堂讲座，对我关于几何思维教学的思考给予了很大启发,使我有关如何 “教”几何思维有了更多的思考.

我在讲授《直线、射线、线段》（第二课时），思考后明确：要“教”的是研究两条线段的思维规律,即:先位置关系,再数量关系.教学中通过学生描述具体操作的方法设计，打通了不同学段知识的逻辑关系,从几何思维的角度看,就是让学生经历了从几何直观到几何抽象的思维过程.研究两条线段就要明确它们的位置关系,之后再用数量关系来刻画这种位置关系.本节课的教学逻辑更加符合几何的学科逻辑。

陈宇老师：在我高中数学教学生涯里，每当讲到《平面解析几何》这一章节，学生都比较犯怵，虽然我费劲去解决，但是收效很一般；今天听完张鹤老师关于《几何思维》的讲座，而后我又把张老师的著作认真地学习了一下，我突然一下子茅塞顿开，对于平面解析几何问题的求解不能只是凭运气傻算，需要对这里面的思维特征有清晰的认识。

①通过研究几何对象的性质，找到代数化的方法。在平面解析几何的研究中，如果研究的对象是一个：如一条直线、一个圆、椭圆、双曲线或抛物线等，那我们就要通过这个对象的代数形式曲线方程，也可以结合它的几何图形、有关的代数值等来研究这个对象的几何性质；再借助这个几何对象的几何性质，选择最恰当的代数方法来解决这个问题。

②通过研究几何对象的位置，找到代数化的方法。

③要选择恰当的代数化的形式。在解决平面解析几何问题时，代数化的方式的选择是非常重要的，选择不当，就会带来计算量的增大，甚至影响到问题的最终解决，其途径更多的来自对几何对象的几何特征的分析。

总之，学习数学的目的是培养我们的数学思维能力，要学好数学，我们就要勤动脑，学会数学的思维方法理解并解决数学问题。思考是一种安静的力量，让我们投入一场数学思维的盛宴中去！